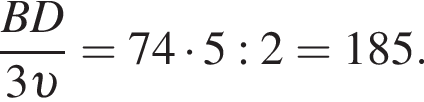Найдите значение выражения 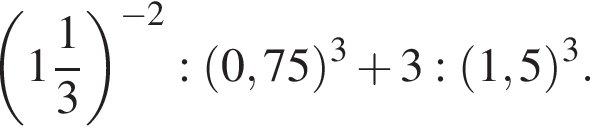
Одно число меньше другого на 64, что составляет 16% большего числа. Найдите меньшее число.
На координатной прямой отмечены точки O, A, B, C, D, F.
Если координата точки A равна ![]() то числу 1 на координатной прямой соответствует точка:
то числу 1 на координатной прямой соответствует точка:
Величины a и b являются прямо пропорциональными. Используя данные таблицы, найдите неизвестное значение величины a.
| a | 1,9 | |
| b | 108 | 7,6 |
Функция y = f(x) задана на промежутке 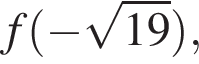
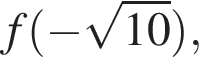
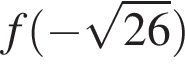 в порядке убывания.
в порядке убывания.
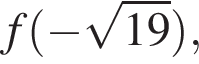


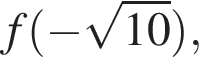
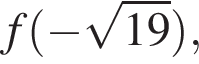
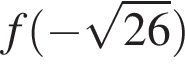

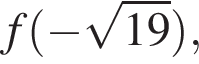


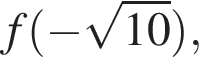

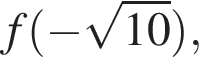


Среди значений аргумента x, равных ![]()
![]()
![]()
![]()
![]() укажите то, при котором значение функции
укажите то, при котором значение функции  меньше
меньше ![]()
Плоскость, удаленная от центра сферы на 8 см, пересекает ее по окружности длиной 12π см. Найдите площадь сферы.
Упростите выражение 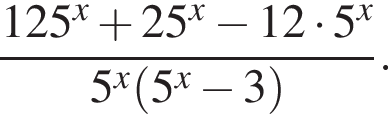
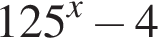
Уравнение 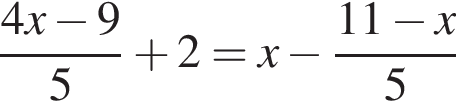 равносильно уравнению:
равносильно уравнению:



Из двух пунктов, расстояние между которыми равно S, одновременно навстречу друг другу с постоянными скоростями отправляются по течению реки плот (П) и против течения реки катер (К). На рисунке приведены графики их движения в течение часа с момента отправления. Определите, за сколько минут от начала движения плот придет в пункт, из которого отправился катер.
Найдите сумму корней (корень, если он единственный) уравнения 
В равнобедренную трапецию, площадь которой равна ![]() вписана окружность. Сумма двух углов трапеции равна 60°. Найдите периметр трапеции.
вписана окружность. Сумма двух углов трапеции равна 60°. Найдите периметр трапеции.
Для начала каждого из предложений A−В подберите его окончание 1−6 так, чтобы получилось верное утверждение.
A) Окружность с центром в точке (−8; −2) и радиусом 4 задается уравнением:
Б) Уравнением прямой, проходящей через точку (−8; 2) и параллельной прямой 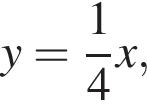 имеет вид:
имеет вид:
В) График обратной пропорциональности, проходящий через точку 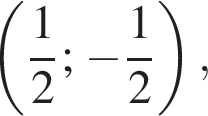 задается уравнением:
задается уравнением:
1) ![]()
2) 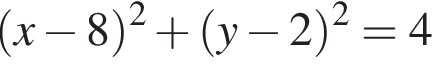
3) 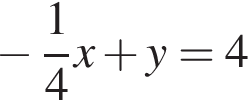
4) 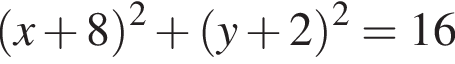
5) 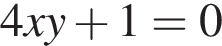
6) 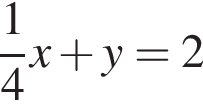
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
Выберите три верных утверждения:
1) если 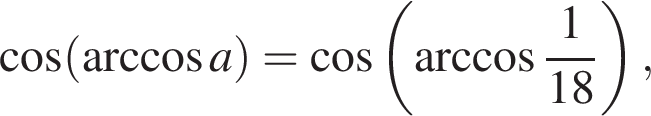 то
то 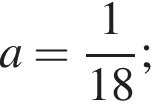
2) если 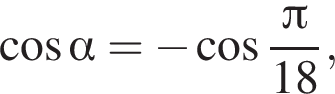 то
то 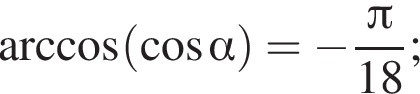
3) если 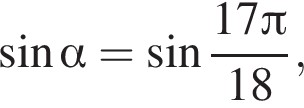 то
то 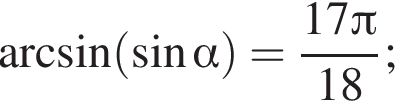
4) если 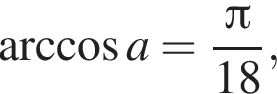 то
то 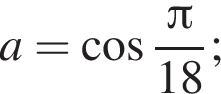
5) если 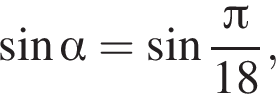 то
то 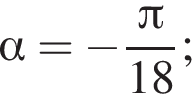
6) если 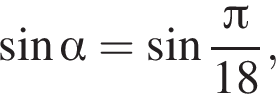 то
то 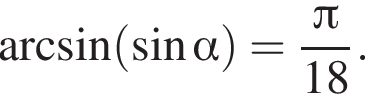
Ответ запишите цифрами (порядок записи цифр не имеет значения). Например: 123.
Градусная мера угла ABC равна 112°. Внутри угла ABC проведен луч BD, который делит данный угол в отношении 1 : 7 (cм. рис.). Найдите градусную меру угла 1, если BO — биссектриса угла DBC.
Найдите периметр правильного шестиугольника, меньшая диагональ которого равна ![]()
Найдите произведение суммы корней уравнения 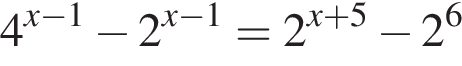 на их количество.
на их количество.
Пусть (x1; y1), (x2; y2) — решения системы уравнений 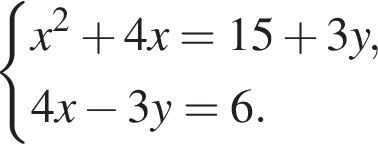
Найдите значение выражения 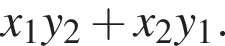
Найдите сумму целых решений неравенства 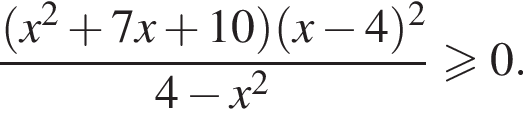
Решите неравенство 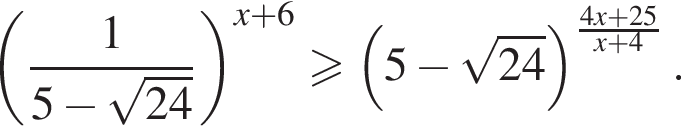 В ответе запишите сумму целых решений, принадлежащих промежутку [−20; −2].
В ответе запишите сумму целых решений, принадлежащих промежутку [−20; −2].
Найдите увеличенное в 9 раз произведение абсцисс точек пересечения прямой y = 12 и графика нечетной функции, которая определена на множестве  и при x > 0 задается формулой
и при x > 0 задается формулой 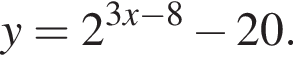
Биссектриса угла А параллелограмма ABCD пересекает сторону ВС в точке К так, что ВК = 2, СК = 3. Найдите значение выражения S2, где S — площадь параллелограмма ABCD, если величина угла А равна 60°.
Найдите произведение всех корней (корень, если он единственный) уравнения
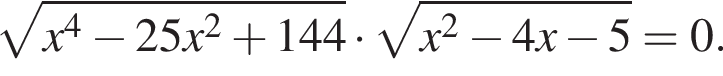
Найдите значение выражения 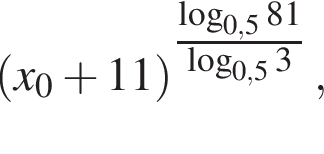 где x0 — корень уравнения
где x0 — корень уравнения 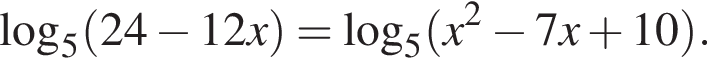
Если 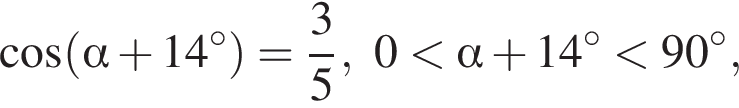 то значение выражения
то значение выражения 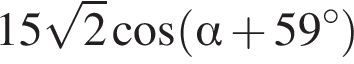 равно ...
равно ...
Пусть 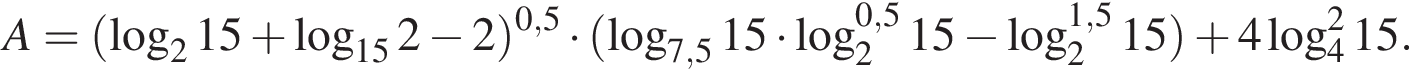
Найдите значение выражения 2A.
Сфера проходит через все вершины нижнего основания правильной четырехугольной призмы и касается ее верхнего основания. Найдите площадь сферы, если площадь диагонального сечения призмы равна ![]() а высота призмы в два раза меньше радиуса сферы.
а высота призмы в два раза меньше радиуса сферы.
ABCA1B1C1 — правильная треугольная призма, все ребра которой равны 3. Точки P и K — середины ребер BC и CC1 соответственно, M ∈ AA1, AM : AA1 = 1 : 3 (см. рис.). Найдите увеличенный в 25 раз квадрат длины отрезка, по которому плоскость, проходящая через точки M, K, P, пересекает грань AA1B1B.
Найдите (в градусах) сумму различных корней уравнения 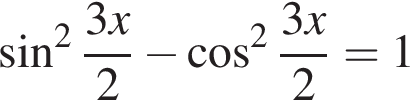 на промежутке
на промежутке 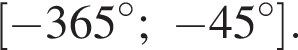
Отрезок BD является биссектрисой треугольника АВС, в котором 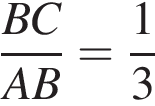 и
и 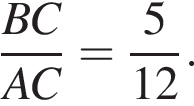 По отрезку из точек В и D одновременно навстречу друг другу с постоянными и неравными скоростями начали движение два тела, которые встретились в точке пересечения биссектрис треугольника АВС и продолжили движение, не меняя направления и скорости. Первое тело достигло точки D на 1 минуту 14 секунд раньше, чем второе достигло точки В. За сколько секунд второе тело прошло весь путь от точки D до точки В?
По отрезку из точек В и D одновременно навстречу друг другу с постоянными и неравными скоростями начали движение два тела, которые встретились в точке пересечения биссектрис треугольника АВС и продолжили движение, не меняя направления и скорости. Первое тело достигло точки D на 1 минуту 14 секунд раньше, чем второе достигло точки В. За сколько секунд второе тело прошло весь путь от точки D до точки В?

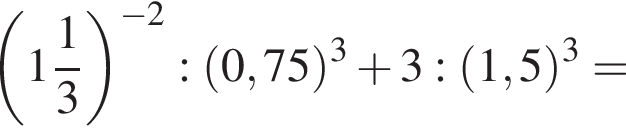

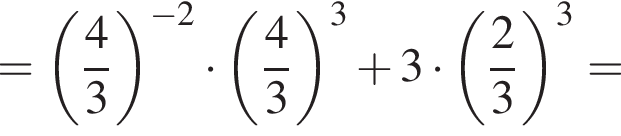
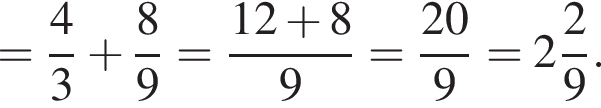
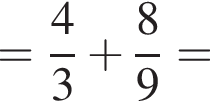
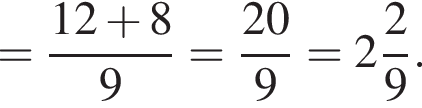
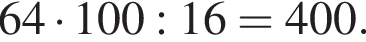 Таким образом, меньшее число
Таким образом, меньшее число 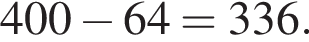
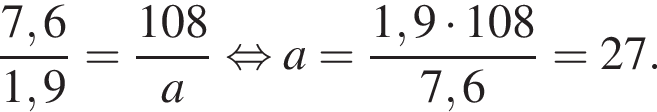
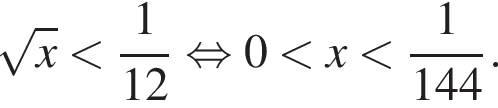 Среди значений аргумента x полученному неравенству удовлетворяет значение
Среди значений аргумента x полученному неравенству удовлетворяет значение  откуда r = 6. Тогда по теореме Пифагора радиус сферы равен
откуда r = 6. Тогда по теореме Пифагора радиус сферы равен 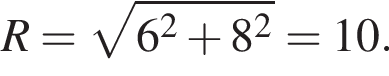 Для площади сферы имеем:
Для площади сферы имеем: 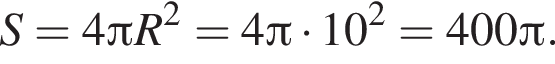
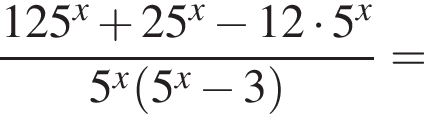
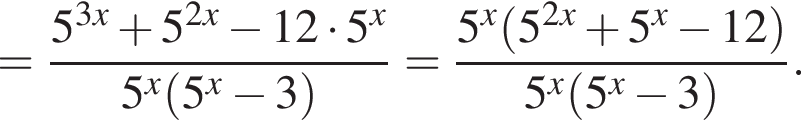
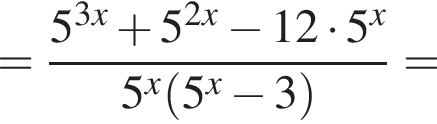
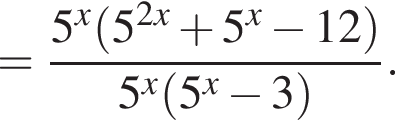
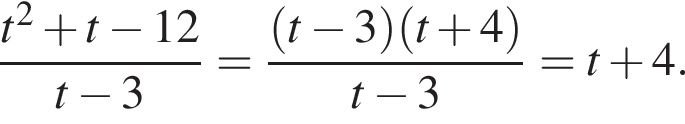 Тем самым, исходное выражение равно
Тем самым, исходное выражение равно 
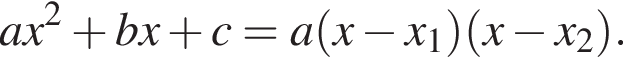
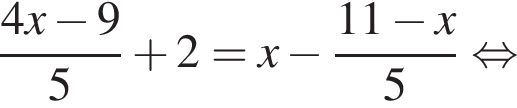
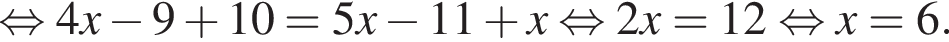

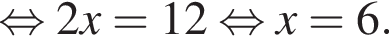
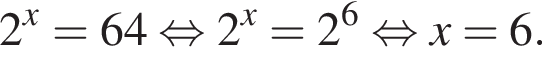
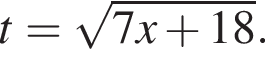 Тогда:
Тогда: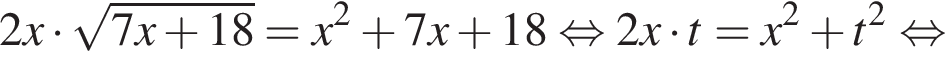

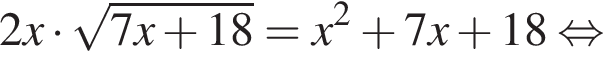


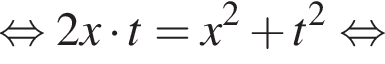
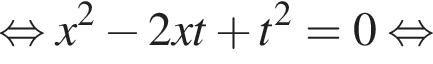
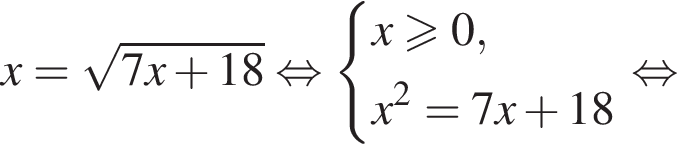
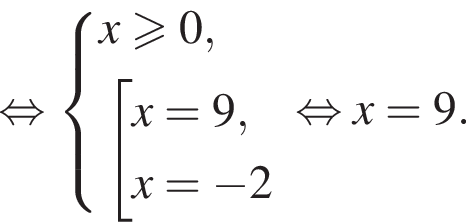
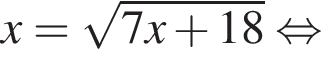
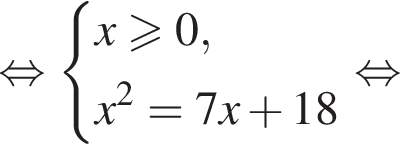
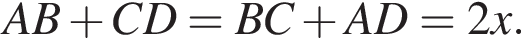 Сумма углов в равнобедренной трапеции, прилежащих к одной стороне равна 180°, откуда следует, что сумма углов, данная в условии — есть сумма углов при основании AD, которые равны.
Сумма углов в равнобедренной трапеции, прилежащих к одной стороне равна 180°, откуда следует, что сумма углов, данная в условии — есть сумма углов при основании AD, которые равны. 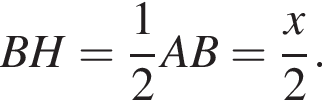 Поэтому из площади трапеции найдем x:
Поэтому из площади трапеции найдем x: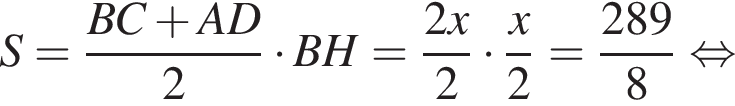
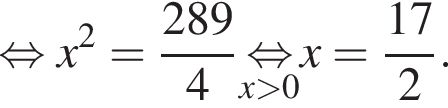
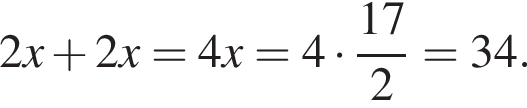
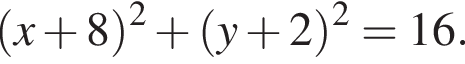
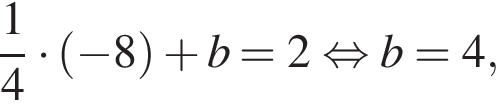 т. е.
т. е. 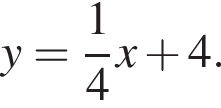
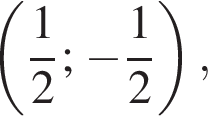 задается уравнением:
задается уравнением:  т. е.
т. е. 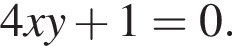
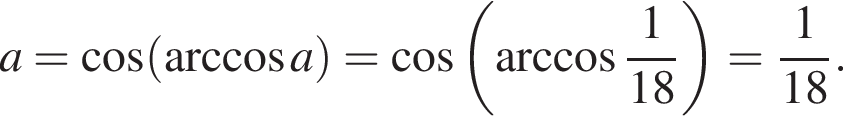

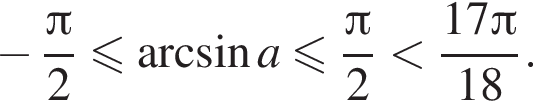
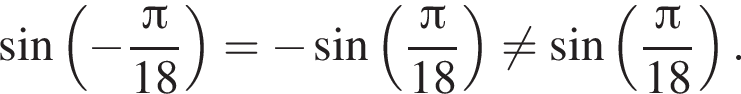
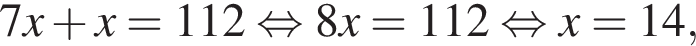
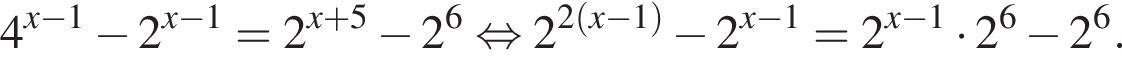
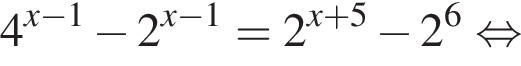
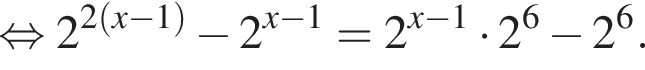
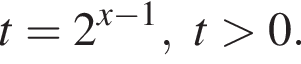 Поэтому:
Поэтому: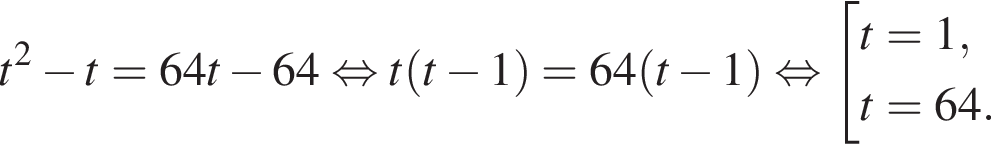

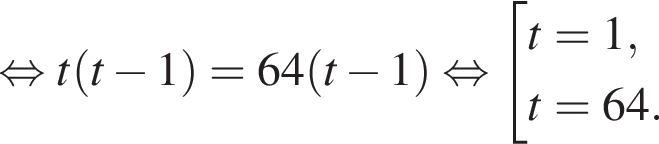

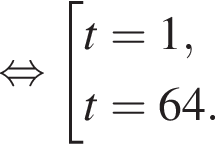
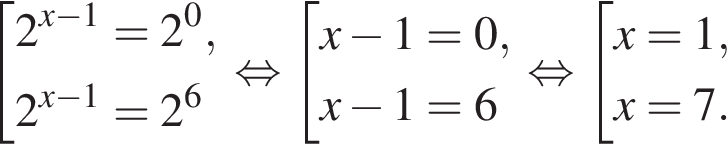
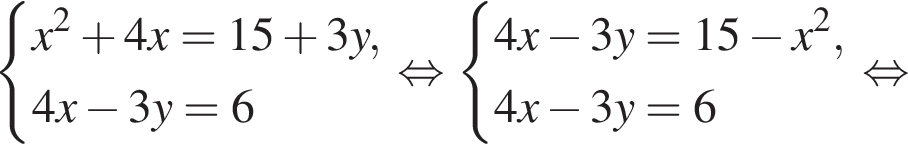
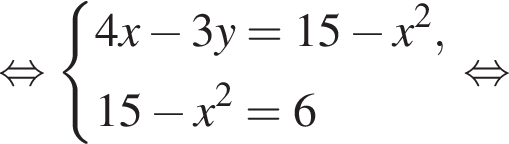
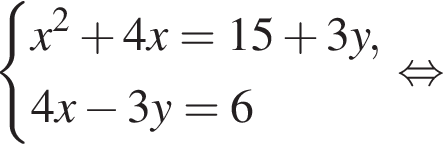
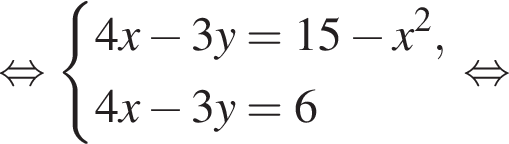
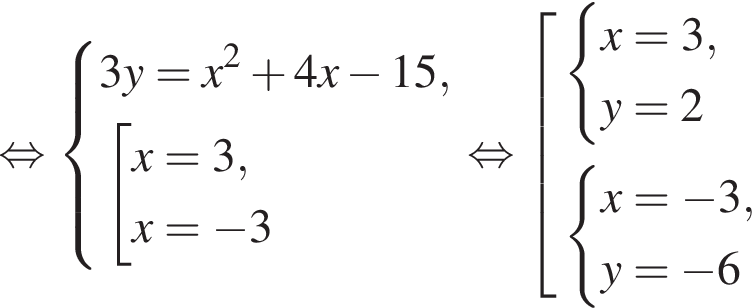

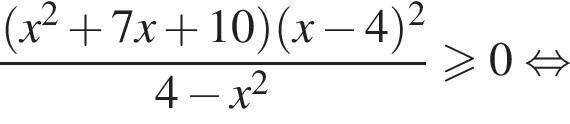
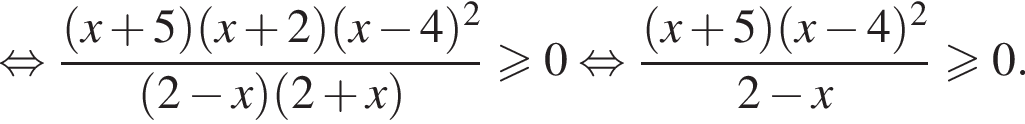
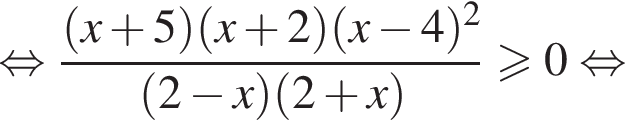
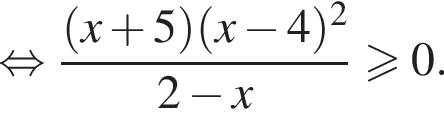
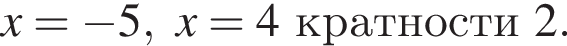 Корень знаменателя:
Корень знаменателя: 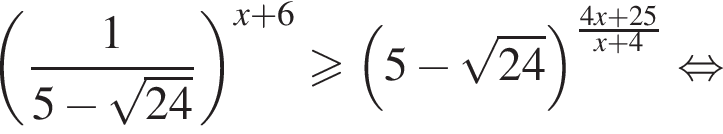
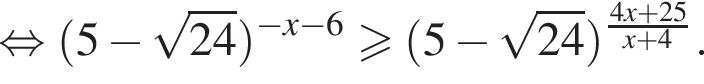
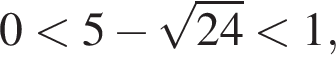 неравенство будет выполняться при
неравенство будет выполняться при 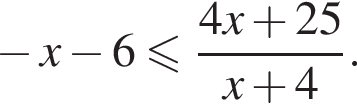 Имеем:
Имеем: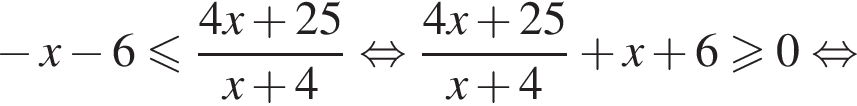
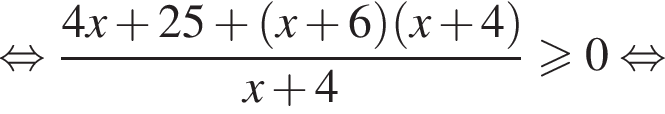
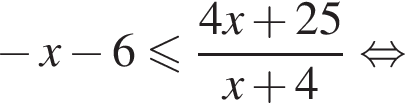
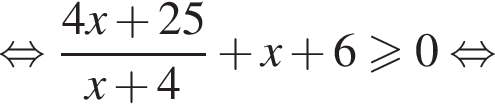
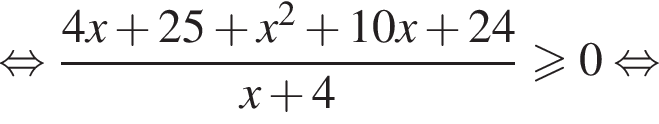
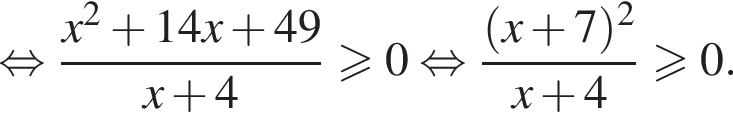
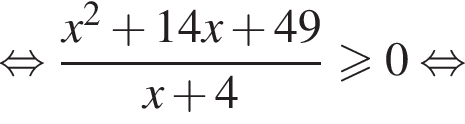
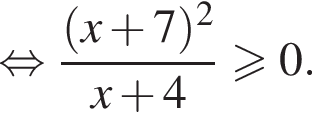

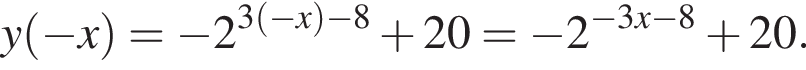
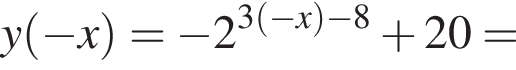
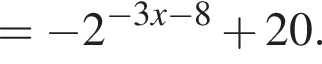
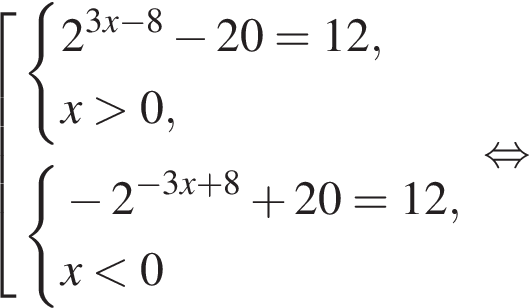
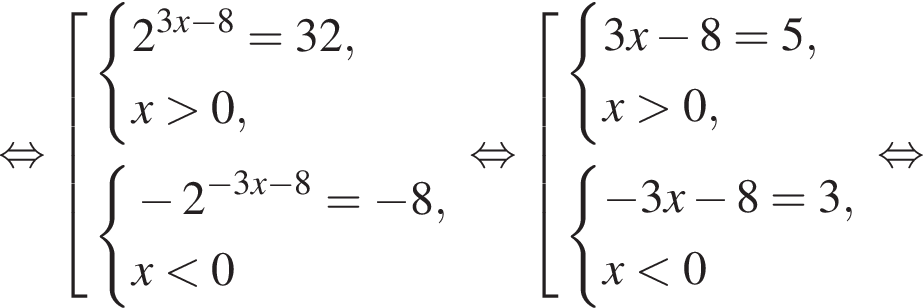
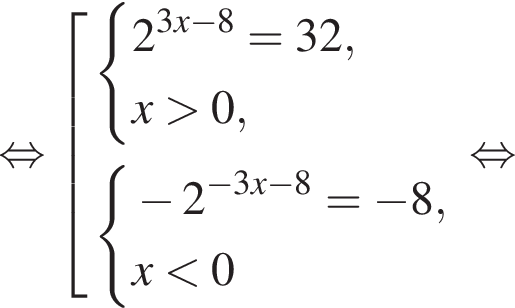
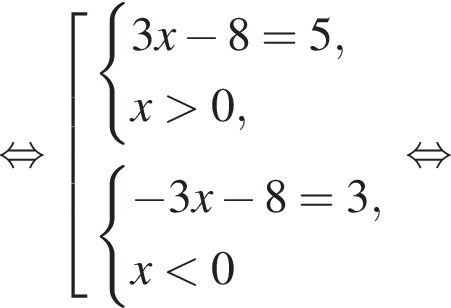
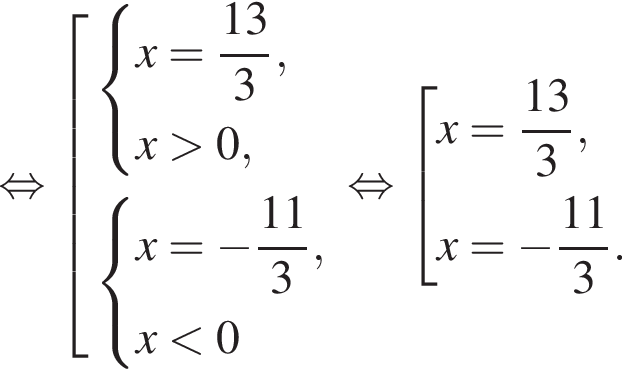
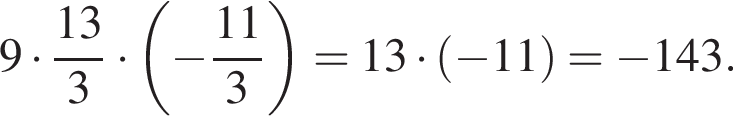
 где первое равенство равно из-за биссектрисы, второе — накрест лежащие углы. Значит, треугольник ABK равнобедренный и потому AB = 2. Далее,
где первое равенство равно из-за биссектрисы, второе — накрест лежащие углы. Значит, треугольник ABK равнобедренный и потому AB = 2. Далее, 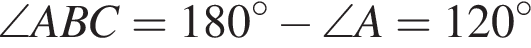 и потому площадь параллелограмма равна
и потому площадь параллелограмма равна 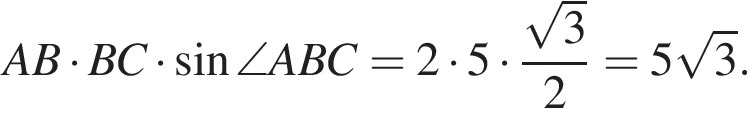
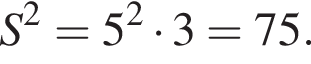
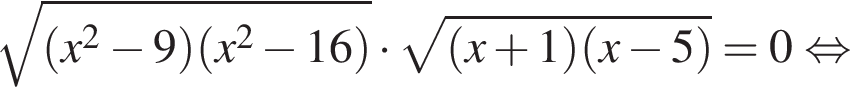
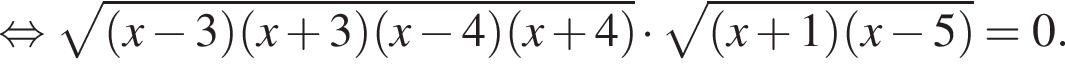
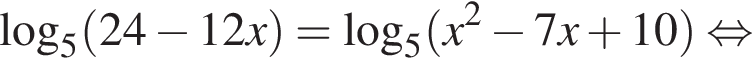
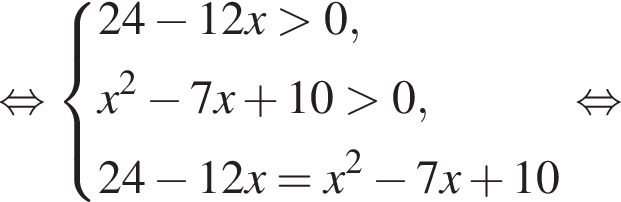
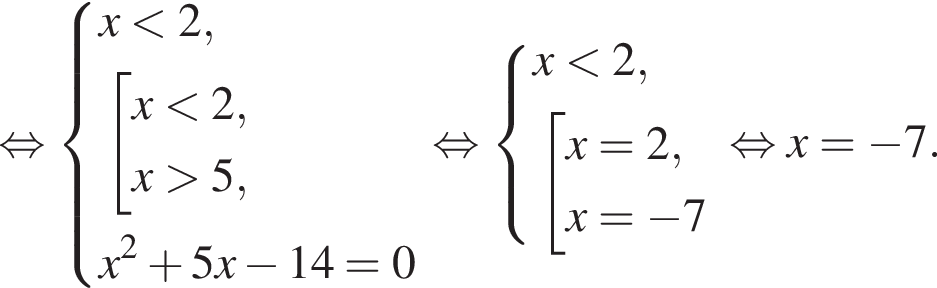
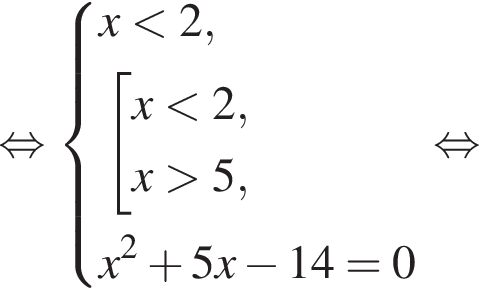
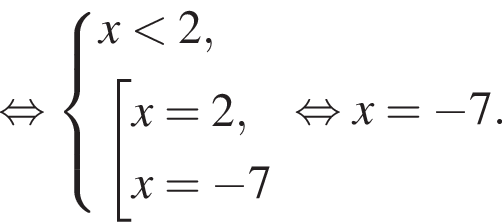
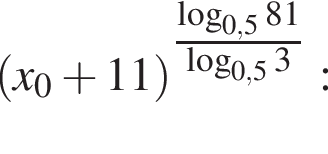
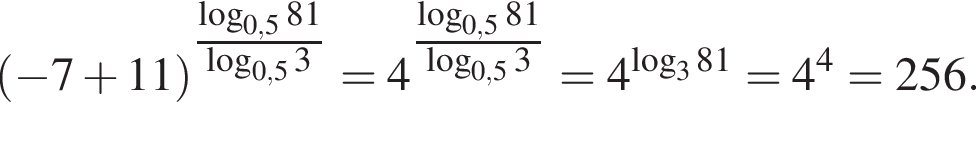
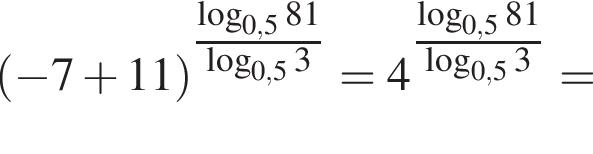

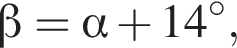 следовательно,
следовательно, 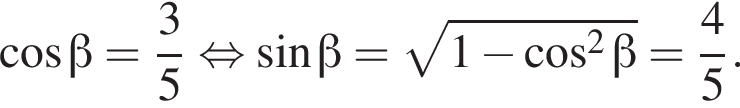 Заметим, что
Заметим, что  Таким образом:
Таким образом: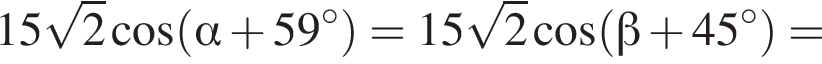
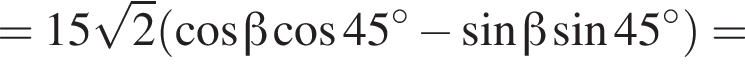
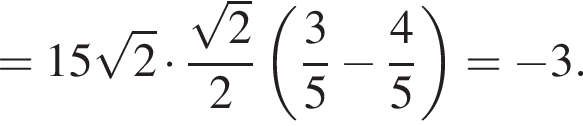
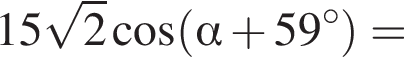
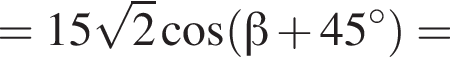

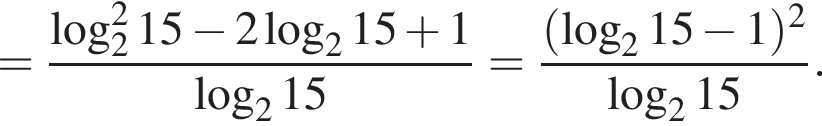
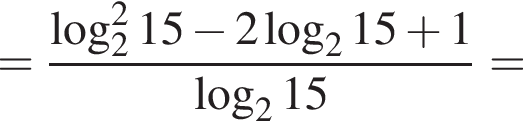
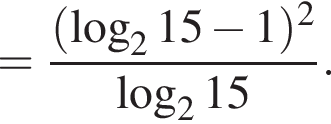
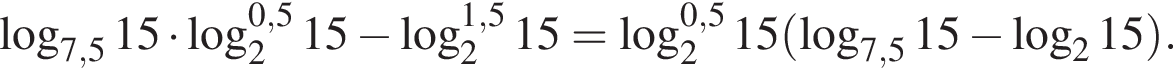
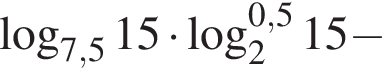
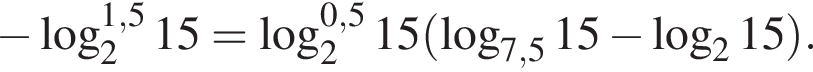
 Тогда имеем:
Тогда имеем: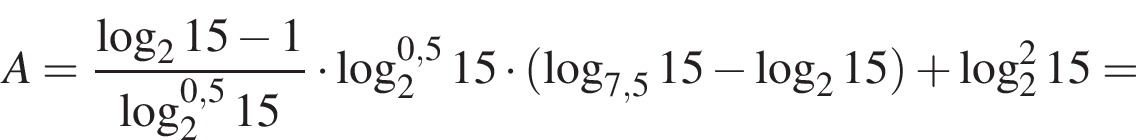
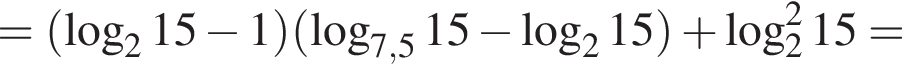
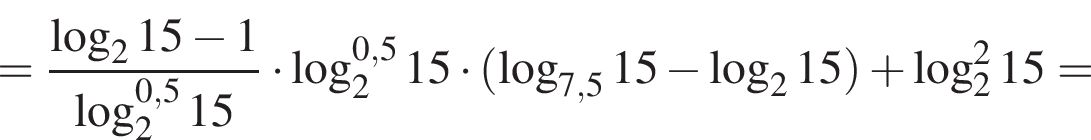
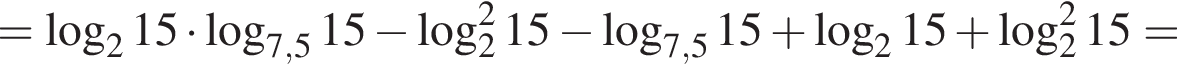
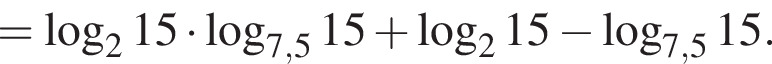
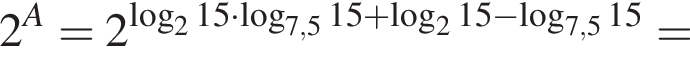
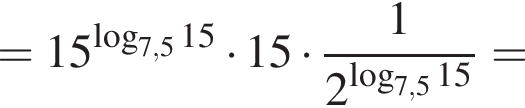
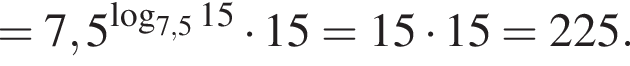
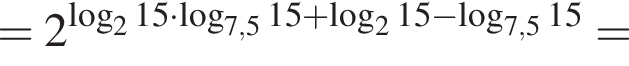
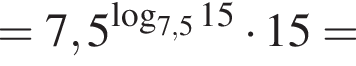
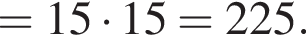
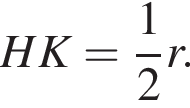 Найдем стороны прямоугольного треугольника AHO:
Найдем стороны прямоугольного треугольника AHO: 
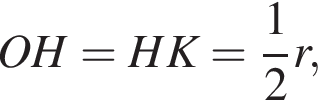 отсюда
отсюда 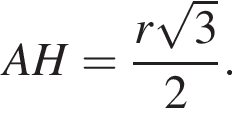 Площадь диагонального сечения
Площадь диагонального сечения 
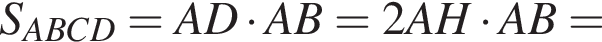
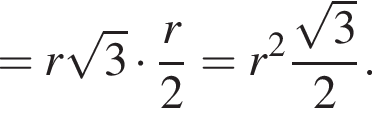
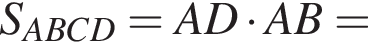
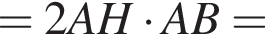
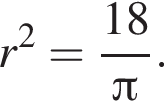 Таком образом,
Таком образом,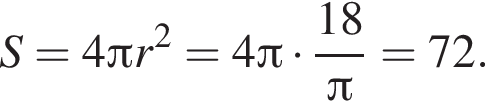
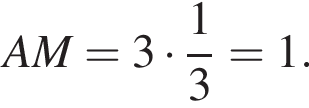 Треугольники KPC и LBP равны по стороне и двум углам, тогда
Треугольники KPC и LBP равны по стороне и двум углам, тогда 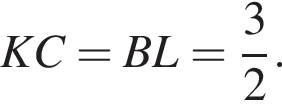 Треугольники BQL и AMQ подобны по двум углам, тогда
Треугольники BQL и AMQ подобны по двум углам, тогда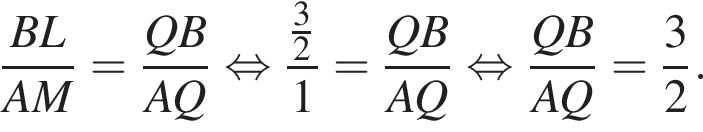
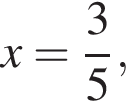
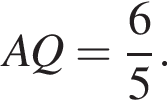 По теореме Пифагора:
По теореме Пифагора: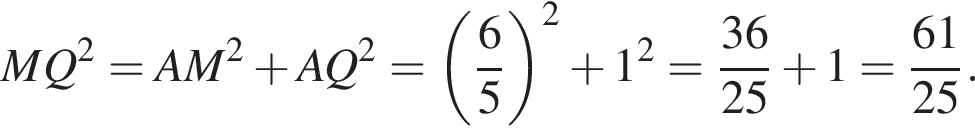
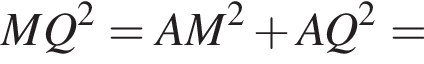
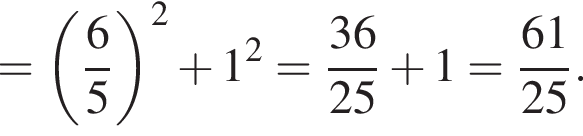
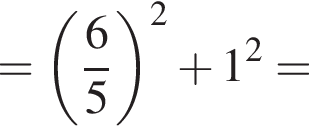
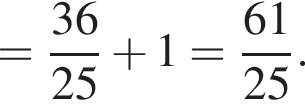
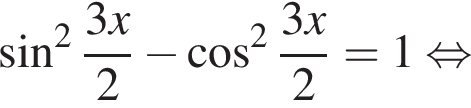
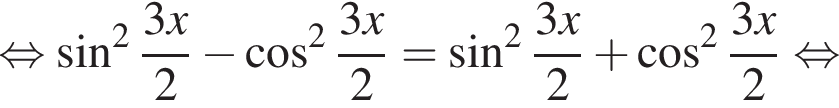
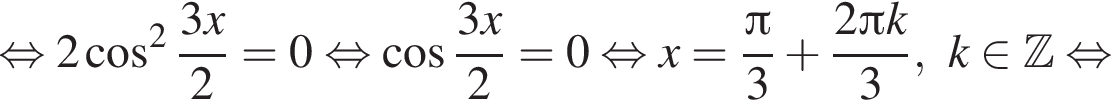
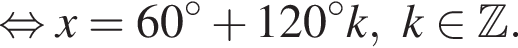
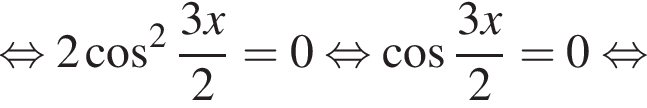
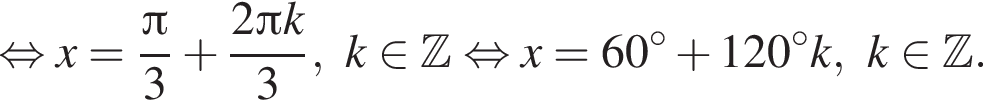
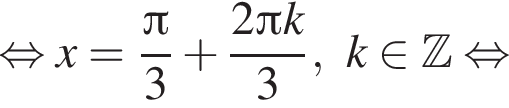
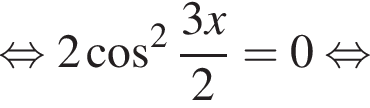
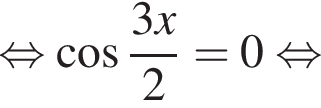
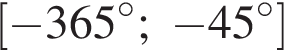 удовлетворяют решения x = −60°, x = −180°, x = −300°, сумма этих корней равна −540°.
удовлетворяют решения x = −60°, x = −180°, x = −300°, сумма этих корней равна −540°.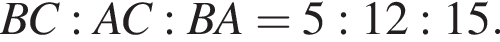 По свойству биссектрисы получаем, что
По свойству биссектрисы получаем, что 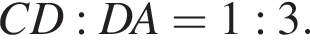 Значит, если
Значит, если  то
то 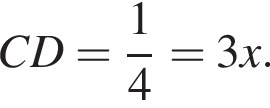
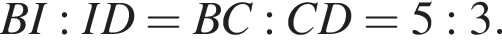 Значит, можно считать, что скорость первого тела равна 5υ, а второго 3υ. Время движения обратно пропорционально скорости, из условия следует, что
Значит, можно считать, что скорость первого тела равна 5υ, а второго 3υ. Время движения обратно пропорционально скорости, из условия следует, что 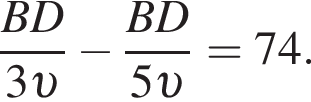
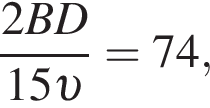 откуда
откуда